时域和频域的转换
一个图表或信号的“域(domain)”,指的是其自变量,通常显示在图表的横轴上。例如,音频波就是一种时域信号,其信号电压或数字振幅随时间而变化。这里的时间就是自变量,因此它通常在波形图的X轴(横轴)上,振幅则在Y轴(纵轴)上。在频域图上,X轴则为频率(Frequency),Y轴为幅度(Magnitude)。除了这两种还有一个例外就是能摄录频谱的摄谱图,它有两个自变量,所以在已知情况下我们围绕任意一个方向讨论都是有意义的。
在录音应用中,时域图上的音频信号显示成波形,它是声音剪辑师的关键视图。然而在音响系统工程和房间声学中,时域(脉冲响应)图上的系统响应可以显示系统本身的传输延时、反射等,但混响会比较棘手。
信号频域的分析提供了频谱视图,在分析声音的音频成分或寻找啸叫点时,这显然是一组非常有用的信息。系统响应的频域视图(传递函数或频率响应)跟用频率分析时间/相位响应一样,提供了一个很容易观察的系统音频响应图像。
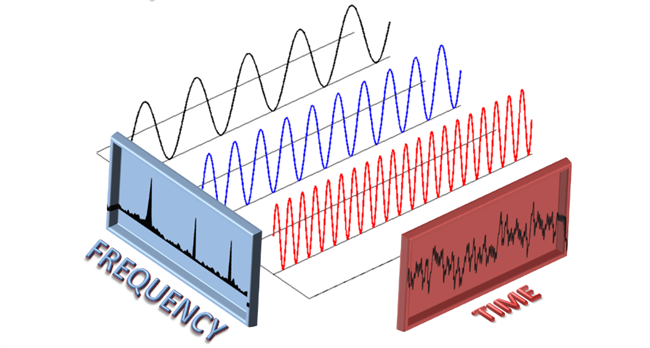
l 时域监控信号随时间变化的幅度。
l 频域按频率监控信号幅值
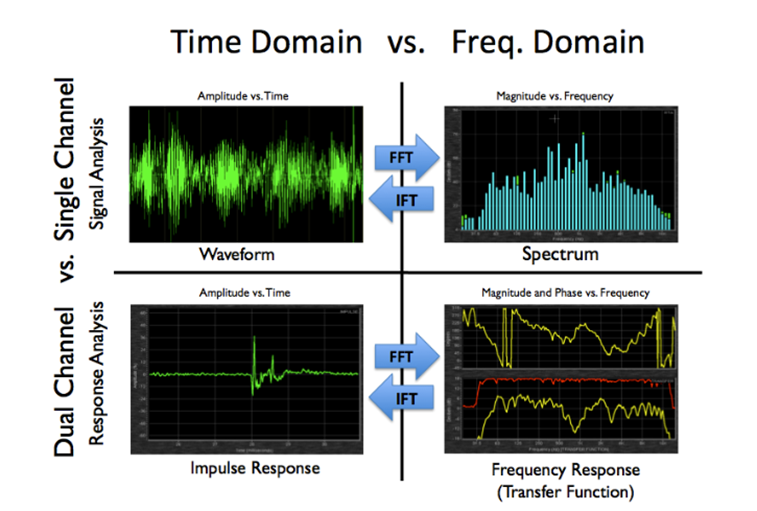
这实际上就是傅里叶变换,其命名于十九世纪法国数学家和物理学家让·巴普蒂斯·约瑟夫•傅里叶。它的概念是:复合信号(如语音或音乐)可以分解为不同振幅和相位关系的正弦波,也可以把它们组合起来。傅里叶变换被广泛应用于音频分析,以发现时域信号的频谱内容。傅里叶逆变换(IFT)是从频谱数据重构时域信号。
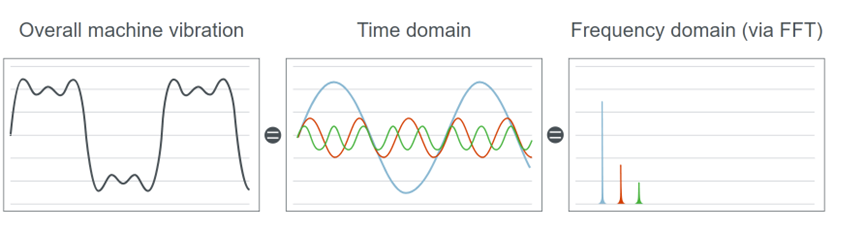
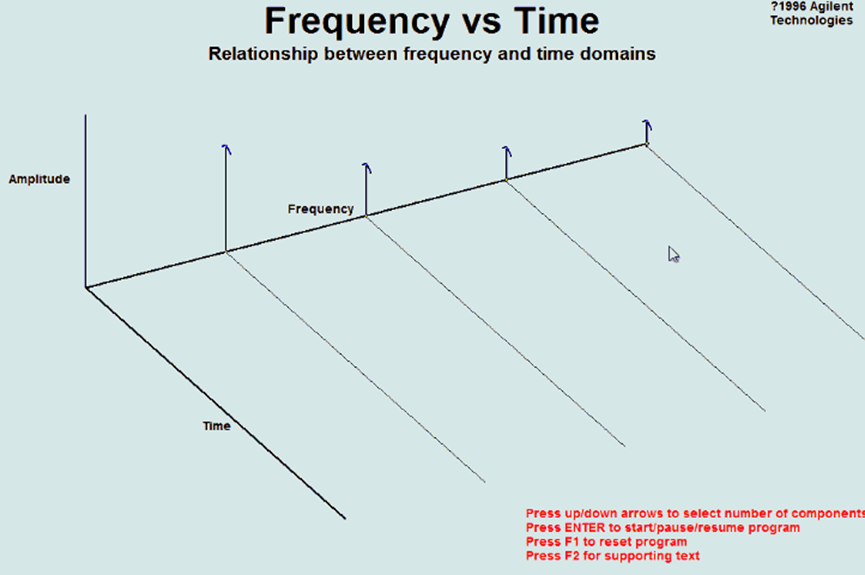
快速傅里叶(FFT)就是傅里叶(IFT)的一种有效计算方法,为分析信号块长度是2的N次幂,如16384(16K,2的14次)。
用记录时域信号的采样率除以「T的采样大小,就可以计算出FFT的时间常数(以秒为单位)。
例如,频谱测量的默认FFT大小为16K(16384)个采样点。以48000样本/秒记录的16KFFT的时间常数为0.341秒(16384/48000)或341毫秒。
𝐹𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑅𝑒𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 = 𝑆𝑎𝑚𝑝𝑙𝑒 𝑅𝑎𝑡𝑒/ 𝐹𝐹𝑇 𝑆𝑖𝑧𝑒 = 1/ 𝑇𝑖𝑚𝑒 𝐶𝑜𝑛𝑠𝑡𝑎𝑛
由于低频的周期比高频的周期长,这正是它们频率低的原因。因此,要用更长的周期时间去来分析低频。事实上,一个FFT(或任何其他类型的DFT)的最低频率就可“看作"”是1/T,在这里T代表以秒为单位的FFT时间常数。比如48k采样率的16K FFT,这个时候频率分辨率为2.93Hz(1/0.341)。


评论区